Real Zeros of Polynomial Functions

Long Division of Polynomials:

We probably all remember long division right? Well, in case you dont here's an example: If we want to divide 8932 by 17 with long division what we would do is 1st see how many times 17 goes into 89, then put that number on top of the bar. Then you subtract the remainder and continue on until 17 can no longer go into the last number. That number is the remainder(in this case 7), we divide this over the original divisor and add it to the quotient. This is the quotient of 8932/17:.
Long division of Polynomials is exactly the same, but with variables for example

/x-1

Would be done like this:

This works, but takes much longer than is necessary.

Synthetic Division of Polynomials:

This is a much more simplified way to find the roots of complex polynomials called synthetic division.

It is set up like this:

Now, what number are you supposed to use as a possible zero? All the possible zeros are the factors of the last term, P, divided by the factors of the first term, Q, like so:

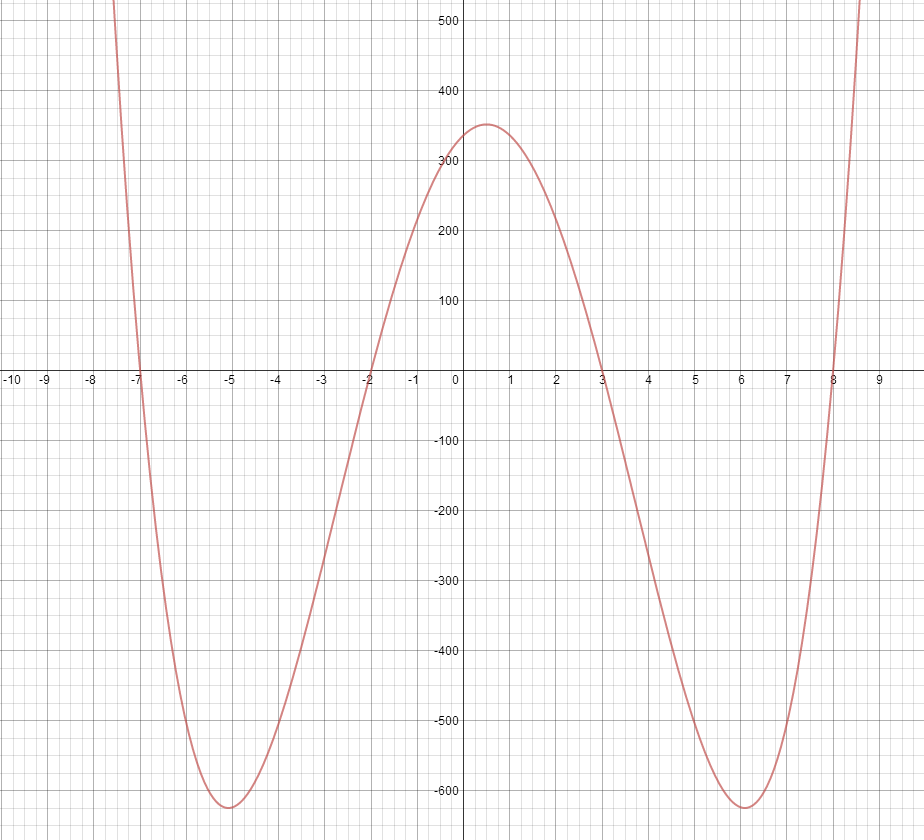
Calculating and plugging in these values, while still a shortcut, would still take ages. Yet again there is another shortcut. If you graph the equation, the points where it crosses the x axis, (zeros/x-intercepts) are the values which you should input, as the remainder will always be 0, meaning it is an x-intercept.

as we can see, the intercepts are, -7, -2, 3,8

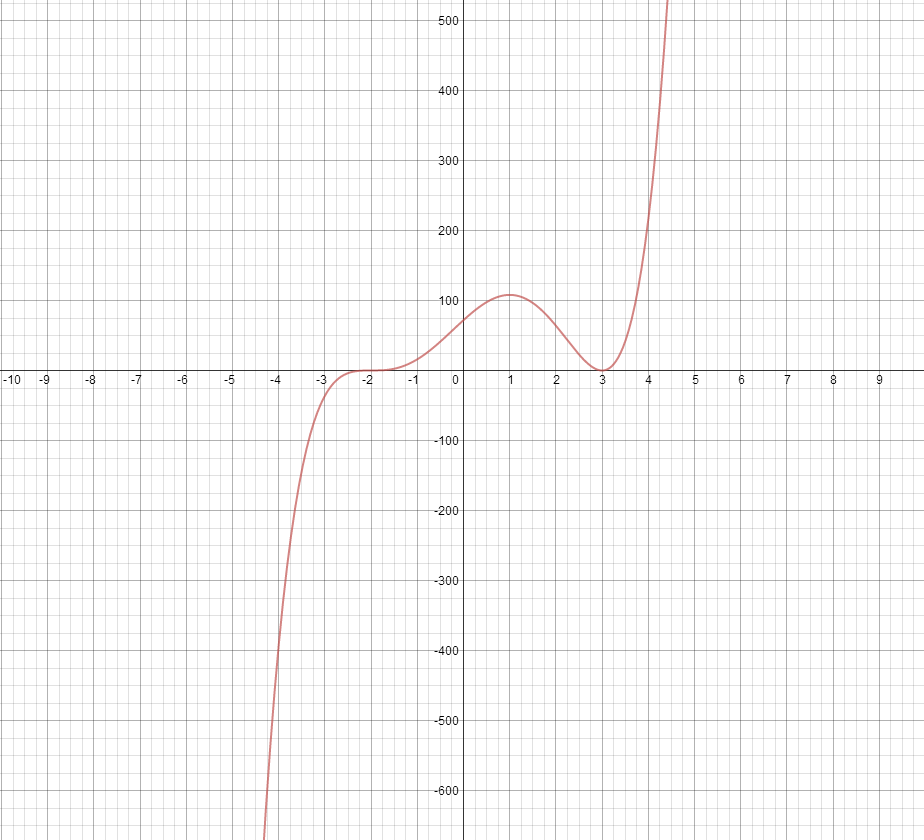
 Repeat this until you have a quadratic( make sure to use the new equation, not the original), then factor the quadratic as normal. It is very possible that if the graph runs tangent to the x-axis, or exhibits some other behaviors, that there are multiples of the x-intercepts like this:

in this case the intercept at (-2,0) has a multiplicity of 3, and at (2,0) has a multiplicity of 2. This means that you must enter the -2 into synthetic division 3 times, and 3 into synthetic division 2 times

Remainder theorem:

Now lets say your teacher gives you an function with many terms. Calculating the value of 

 

would take forever. However the remainder theorem states that that if a polynomial  is divided by

the remainder is

you thought there wouldn't be scrolling text, but there was