First, you can set up the equation:
Then, subtract logb from both sides:
Next, using the definition of a logarithmic function you can change it into this form:
Subtraction in the exponents means you can change it to this:
The denominator can then simplify:
You can multiply both sides by b:
You can then take the log of both sides:
You can use these properties to expand or simplify/compress logarithmic expressions:
Expanding:
Simplifying:
There is also the change of base formula:
To prove this formula:
First, you can set up the equation:

and change it to:
Next, take the log of both sides; it does not have to be base 10:

Using the properties of logarithms:

Divide:

One common mistake that people make its they think log(a+b) = loga + logb. This is NOT true!







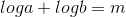






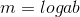
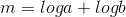















No comments:
Post a Comment